Newton, tvůrce klasické mechaniky, která se stala základem mechanického materialismu, věřil ve stvořitele. Vedle horlivého zastánce materialistického nazírání L. Boltzmanna, jednoho ze zakladatelů kinetické teorie, žije idealistický pozitivista E. Mach, z jehož pera vzešla první vážná kritika Newtonovy mechaniky.
N. Bohr, jeden z těch, kteří pomohli vytvořit kvantovou teorii, rozvíjí Machovy myšlenky, kdežto A. Einstein, tvůrce teorie relativity, nezadržitelně spěje k materialistickému pojetí přírodních dějů. A. Eddington, který píše významné práce o vývoji a stavbě hvězd a o TR, je bojovným idealistou, kdežto materialista A. A. Fridman vypočítává tvar vesmíru podmíněný gravitační interakcí, oba užívají téhož aparátu, téže teorie.
Ivan Úlehla Od fyziky k filosofii. Orbis, Praha 1963, s. 268
I. Poznání a matematika
Zacyklení vývoje pozemských civilizací není prospěšné. Lidstvo, snad jedno z mnoha podobných ve Vesmíru, může opustit smyčku cesty: zadýchaně nahoru a potom rychle dolů.
Poznání těší zvídavé lidi; čím překvapivější, tím zajímavější. Duchovní poznání bylo snad fenoménem našeho dětství, kdežto pak z poznávání karmy, taoismu a spravedlnosti vystřízlivíme? Ne, přechod od náboženství k materialismu postihl naše pradědy. Dnes sledujeme opačnou tendenci.
Souhlasíme-li s názorem, že základem všeho je slovo – myšlenka, pak se nabízí hledat podobný přístup i pro konstrukci Vesmíru. Nevznikl ze zázraku a zřejmě ani z nesestrojitelných nekonečen.
Jak je mozku příjemné opájet se proudem objevných vět o našich chybách, o inkarnacích a transformacích – od znale sdělujících autorů. Postačuje sledovat jejich myšlenky a ani se k nim nemusíme vyjádřit.
Je nám potřeba více přemýšlení, jenže to bolí – podle TGM!
II. Objevit smysl
Svět poznáváme právě svými smysly. Pomáhají jim experimentální obory, které jsou stále vyspělejší. Pouhými smysly nerozlišujeme, zda se hmota skládá z atomů, či zda je celistvá.
Nejdůležitějším sudím různých přístupů a jejich výsledků pak bývá matematika. Jistě spravedlivě hodnotí oprávněnost závěrů. Přesto, čím však posuzovat, jak se závěry shodují se skutečností? Až mechanický model zpracovává výsledek znovu ku smyslovému posouzení.
Vědě bývá potřebné, aby ten který obor byl matematizovatelný. Když psychologie hůř vyhovuje matematickému zhodnocení, pak je obtížnější prověřit její výsledky, než tomu je v oboru mechaniky. Studovat vlastnosti člověka a vztahy mezi lidmi není snadno přístupné – ve srovnání s hmotnými problémy.
III. Zážitky
Chuťové zážitky z předkládaných pokrmů dovedeme sledovat ostražitě. Vyhodnotíme důsledky pro zdraví a podivný pokrm vyplivneme.
Jak vyhodnocujeme zrakové zážitky? Jejich matematické prověření je potřebné i v geometrii; zrakové vjemy mají co sdělit o našem světě. Mám zato, že vyhodnocení matematických závěrů geometrie nebývá dost důsledné. Dosud se dává přednost geometrii, která je ze smyslových vjemů odvozená. Naše víra ve snadno pochopitelnou Euklidovu geometrii trvá už od starověku.
V dalším posuzuji, jak důkladně fyzika prověřila geometrické poznatky výpočtem.

Obr. 1. Několik předmětů
Ve vědomí máme zrakový zážitek několika jakýchsi předmětů (obr. 1).
(Počítání na prstech dává vzniknout počtům.)

Obr. 2. Zraková perspektiva
Zrakový zážitek, který vznikl ze shodných předmětů, bývá dítěti zprvu překvapivý (obr. 2). Stejný předmět v dálce je malý. Není malý? Ale, vždyť ho vidím malý?
(A jak nahradit počítání na prstech a zvládnout výpočty i s většími čísly? Římská číselná soustava použila zkratky. Nahradila skupinu několika čárek novým znakem. Pět prstů IIIII označila V, deset prstů IIIIIIIIII nahradila X, atd. Znaky spolupracují poněkud náročně; někdy se jejich hodnoty sčítají (XII = 12), jindy odčítají (IV = 4)).
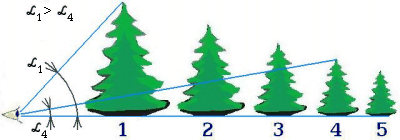
Obr. 3. Zorný úhel
Změnu velikosti zrakového zážitku může zdůvodnit zorný úhel, protože vzdalovanému předmětu se zmenšuje (obr. 3).
(A jak počítat s velkými čísly? To bylo umožněné zařazováním číslic do řádů. Číslici chybějícího řádu možno vynechat, anebo ji zastoupit nulou. Tato věta je poněkud kacířská. Snad uvažuje, že nula není stejné číslo, jako jsou ostatní?
Například jedentisícosmdesátsedm 1.087 = |1| |8|7|. Tabulka by užívala vyhrazené buňky pro dekadické řády, zde by byly čtyři |1000|100|10|1|). Zajisté, místo této tabulky pro psaní čísel je lepší vynalézt nulu.)
Perspektivní zmenšování však nezdůvodním jen zorným úhlem Euklidova prostoru. Vysvětlení vnáší svými metodami také informatika. Jsme schopni nestranného vyšetření našeho světa?

Obr. 4. Datový proud
Tvor vnímá perspektivní prostor. Příslušné vjemy mu zajišťuje datový proud, který bývá odhadován pro všechny lidské smysly kolem 10 megabitů za sekundu (obr. 4). Může být konstrukce datového zdroje našeho života předem promyšlená nebo nemůže?
Ostatně, co je to život? Nabízím – život je vědomé ovládání hmoty. Život je ovládání hmoty vědomím. Této alternativní charakteristice života vyhovuje jak nezničitelná hmota v Euklidově prostoru, tak i svět – matrix, uměle připravený vyšší Civilizací, kterou odedávna někteří lidé předpokládali. V matrixu je hmota jen smyslovým zážitkem.
Tato definice přisuzuje vědomí také stromům, rostlinám. I u nich rozlišujeme, zda jsou či nejsou živé. Naopak podle základní představy žádné housle, počítač nebo rozvodná síť vědomí nemají, pak tedy živé nejsou. Nevím, zda mají nebo nemají.
Perspektivní zmenšování běžně zdůvodňujeme zorným úhlem, který užíváme v Euklidově prostoru. Druhou možností je hotový perspektivní obraz. Může být braný z neprozkoumaných zdrojů a přiváděný rovnou do vědomí, obsažený v toku 10 Mb/s.
Důvěryhodnost těchto dvou případů posoudím srovnáním. Prověřím, jak dobře vyhovují matematizaci. Lze více důvěřovat prostoru Euklidově anebo perspektivnímu?
IV. Užívání Euklidova prostoru
Čtverce nad odvěsnami mají dohromady stejný povrch jako má čtverec nad přeponou. Ukazují to trojúhelníky na čtverečkované ploše (obr. 5). Prokazují to?

Obr. 5. Povrchy čtverců dle Pythagorovy věty
Připomínám, že je to hypotéza, přijatý názor, protože toto nám zrak nesděluje! Shodný součet povrchů si jen myslíme. Pohled na obrázek je totiž perspektivně zkreslený. Jsou-li trojúhelníky v rovině, pak nám zrak rozhodně nepředává do vědomí tyto obrazce jako stejně velké.
Skutečnost ať prokáže matematika.
Pythagorovu větu vyjadřuje rovnice a2 + a2 = u2. Čtverec ať má stranu délky a = 1, takže k výpočtu úhlopříčky u je nutné vyřešit rovnici: u · u = 2. Nekončící výpočet, s neustávajícím upřesňováním výsledku, umožnil matematice zavedení iracionálních čísel.
Výpočet neprokazuje platnost Pythagorovy věty (obr. 6). Pro žádný čtverec se nepodaří vypočítat jeho úhlopříčku. Důležitost matematiky selhává v Pythagorově větě? Ne.

Obr. 6. Matematizace Euklidova prostoru
Soudím, že chybějící racionální čísla v nekončícím výpočtu nijak neselhávají! Matematika nedává konečný výsledek. To značí, že Euklidův rovnoměrný – lineární prostor není ve hmotě uskutečnitelný. Můžeme v něj pouze věřit. Lze s ním velmi úspěšné pracovat ve speciálně připravené a pojaté matematice.
Jenže fyzika se zabývá popisem našeho světa. Euklidův prostor je matematice prospěšný, následně slouží i fyzice. Avšak právě fyzika ať posuzuje, zda je či není takový prostor geometrií našeho světa. Takové rozlišení matematiku nemusí zajímat. Zavedená matematika infinitesimálních hodnot je prospěšná, ale neprokazuje způsob existence světového prostoru.
Kacířský závěr, odmítnutí Pythagorovy věty, vyznával Giordano Bruno (1548-1600); upálený byl však za něco jiného. Doporučoval ve své době i odlišné duchovní přístupy, než jenom ty převládající.
V. Matematizace
Nevyřešíme matematicky, zda určitý fotbalista dá v dnešním střetnutí branku nebo zda nedá. Nějaká pravděpodobnost nás neuspokojí a tak není co počítat. Tam chybějící matematizaci nevidím. Podmínky života nám ji nenabízejí.
Ale s matematizací Euklidova prostoru je tomu jinak. Mnohé vlastnosti této geometrie známe, jenže některé výpočty v ní nedají výsledek. Staleté zdůvodnění sdělí: délka úhlopříčky je iracionální. Anebo: strana čtverce a úhlopříčka jsou nesouměřitelné. Jenže to je jen pojmenováním či popisem problému. Ale není to zdůvodněním nemožnosti, proč nespočítáme přesnou vzdálenost dvou bodů. Vždyť jejich geometrická vzdálenost je konečná. Přemítám: proč není konečný i výpočet?
Euklidův prostor není matematizovatelný. V něm není možné spočítat vzdálenost některých dvou bodů, proto tato geometrie nemůže být obrazem hmotného světa. Euklidův prostor zůstává hypotézou – domněnkou.
Jistotou je zážitek perspektivního prostoru.
VI. Datový proud z databáze
Uvažuji, že do tvorova vědomí je vkládaný hotový obraz – perspektivní (obr. 7). Související vjemy hmoty pak můžou být životní virtuální realitou.
Obrázek má přepočítané původní souřadnice lineárních os, jsou umocněné na druhou. Místo Euklidových 0 – 1 – 2 – 3 (červeně) připisuji umocněných 0 – 1 – 4 – 9 (modře).
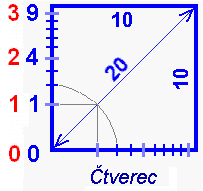
Obr. 7. Matematizace perspektivního prostoru
Náš svět má svou perspektivní geometrii, kdežto údaje v datové paměti počítače nebývají nějak nelineárně stlačené. Bývají to údaje diskrétní – o bodech. To lze splnit i pro náš svět a tím ho přiblížit počítačové virtuální realitě. Zjišťuji, že diskrétní (bodový) prostor lze přepočítat do prostoru kvadratických souřadnic (obr. 8). Takže získávám prospěšnou souvislost. Body z prostoru diskrétního lze převést do perspektivního a přitom jim dodržet jak vzdálenost od počátku, tak i všechny kartézské souřadnice, např. x, y, z.
Naopak prokázat takovou spolupráci diskrétního a Euklidova prostoru je vyloučeno.
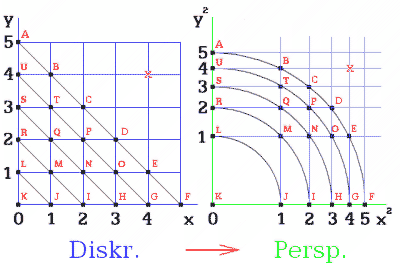
Obr. 8. Převod z prostoru diskrétního do „spojitého“ perspektivního
Odedávna naměříme úhlopříčce čtverce a = 10 metrů délku asi 14,1 metru (obr. 6). Jak obhájím, že úhlopříčka má 20 metrů, podle perspektivy (obr. 7)? Popíšu, jak perspektivní prostor ukazuje náš svět a jak je matematizovatelnou alternativou prostoru Euklidova.
VII. Zdůvodnění perspektivní skutečnosti
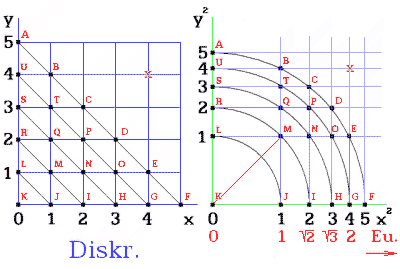
Obr. 9. Zdůvodnění racionální úhlopříčky čtverce
Když použijeme dvě metrové tyčky, pak jsme zvyklí jejich délku počítat v Euklidově prostoru. Nabízím, že Euklidův prostor není. Pak zdůrazňuji to, co vidíme.
Jako matematizovatelný svět prověřuji ten perspektivní – černá čísla (obr. 9). Dvě tyčky početně zpracuji v obrázku napravo, první v délce 0-1 a druhou v délce 1-2, to je úsečka KI. Když ji pootočím z osy x2 o 45°, vznikne úsečka KM. Nadále je její délka 2 m, stlačená perspektivou. Úhlopříčka KP čtverce KIPR měří 4 metry – v perspektivě – černá čísla.
My si však vymýšlíme lineární neskutečný prostor, takže první tyčku správně měříme délkou 0-1, ale té druhé vymyslíme nový prostor. V něm jí chybně přisuzujeme červenou délku 1-2 Euklidova prostoru, tomu odpovídá 1-4 na kvadratické ose.
Ve vymyšleném Euklidově prostoru máme čtverec KGXU. Myslíme si, že žijeme v existujícím hmotném světě a že tedy vzdálená tyčka má stále svou délku 1 m.
Pokud obě tyčky, dosud jakoby položené z bodu K do G (délka Euklidova 0-2 nebo perspektivní 0-4), nyní pootočím do úhlopříčky, pak začínají v bodě K a končí v bodě P. Euklidův prostor jim vypočítá anebo nevypočítá délku dvou odmocnin ze dvou? Tedy (2 * sqrt(2))? Nevypočítá!
Zásadně jsme zvyklí používat Euklidův prostor, ačkoliv náš svět je světem perspektivním. Při uvažování konstrukce světě je třeba užívat délky perspektivního zobrazování.
Nadále má člověk nutkání namítat, že vzal dvě metrové tyčky, nasměroval je úhlopříčně a ony dávají… Jenže hmota je iluze, matematika prokazuje, že máme dbát zraku. Vyrobená tyčka není z pevné hmoty, skutečností je iluze tyčky, která „gumově“ mění svou délku.
VIII. Zhodnocení perspektivního prostoru
Uvažuji, že informace o našem světě jsou uskladněné v diskrétní databázi. Její skutečné geometrické uspořádání není podstatné. Podobně je lhostejné, zda jsou data pro počítač pamatovaná v soustředných kruzích na magnetickém kotouči, nebo zda je schraňuje polovodičová paměť lhostejného tvaru.
Pozice pro uskladnění bodů lze označit přirozenými pořadovými čísly. Pak rastr perspektivního lidského vjemu má osy, které se vytvoří umocněním přirozených čísel na druhou. Body, přenesené z diskrétního do perspektivního prostoru, dodržují vzdálenost od počátku. Současně dodržují i kartézské souřadnice, převzaté z os diskrétního prostoru (obr. 8).
Naopak informace z diskrétního prostoru nelze přenášet do Euklidova. Údaje se přenášejí mezi systémy diskrétní databáze – perspektivní zážitek, a mezi nimi nemá prostor Euklidův žádné uplatnění.
Diskrétní prostor, v návaznosti na perspektivní, umožňuje zdůvodňovat základní poznatky speciální teorie relativity. Ty jsou dosud brané výhradně axiomaticky.
Diskrétní prostor umožňuje zpřístupnit smyslům konstrukci vícerozměrných prostorů.
Náš svět není provedený Euklidovou geometrií a jistě ani z ní odvozeným zakřiveným prostorem. To je sdělené – zaručené matematickým výpočtem. Kdežto měření délky připouští obě možnosti. Preferuji tu možnost, která vyžaduje měření z počátku souřadnic, kdy se pozorovatel nikam nepřesunuje.
IX. Informace
Žil kdysi nadaný pán a měl kolem sebe dva bratry, stejně směrované. Kde ho dál hledat, snad mu někde porozuměli a přijímali ho? Mohli by dva bratři, kteří před desítkami let byli mnohonásobnými sportovními mistry světa, mohli by být chápaní jako hrdinové? Podobní středověkům rytířům? Může být nadčasovým géniem třeba fotograf?
Může se snad zvednout upadnuvší závodník, a znovu v závodě nabývat vrchu? Má na to patent? Rozhoduje tah na branku, nebo něco skrytého v lidských osudech?
X. Berdej
Roztočený osmihran (obr. 10.), zakončený hrotem i držátkem, nabízí náhodně: BER, a jindy zase: DEJ. Nelze se zdržet – nebrat a nebo nedávat. Pravidla určují jinak. Nebo jen radí?
Obr. 10. Berdej
Hráč zatočí berdejem, ten zpomaluje, až spadne. Po zastavení si hráč přečte pokyn na horní ploše berdeje. Po přečtení výsledku neudělá nic?
Kromě pokynů DEJ 3 či BER 1 se vyskytne i BER VŠE. I to je v životě možné, bez ohledu na ostatní hráče. Ale někdy také VŠICHNI DAJÍ. Promyšlená pravidla nabízejí oba přístupy k existenci.
Pokyn BER VŠE je podobný zastaralému přístupu, kdy jednomu přisvojili celou zemi. Co zbylo ostatním? Nápis VŠICHNI DAJÍ učí civilizaci několika lidí, při hře o zápalky, zapracovat společně.
Věda nás všech je dosud lhostejná k nalezení příčiny iracionalit. Nejsoucí vzdálenosti, budou-li nadále nejdůležitější, určí v konečném důsledku tragédii politiky, ekonomie, zakrnělé kosmonautiky a budou katastrofou lidských vztahů.
Bohumír Tichánek
http://www.tichanek.cz/


