Od lovu mamutů jsme došli k lovení asteroidů. Jejich objevy nás mohou ochránit před nebezpečím při pádu na Zem. Ovšem dál pak musí navázat chránící kosmonautika.
Řádná i mimořádná poznávání světa souvisí s biologií, fyzikou, psychologií a dalšími vědeckými obory. Naši smyslovou výbavu pro zkoumání světa podporují stále lepší přístroje. Prodlužují lidské smysly. Naše desítky zkoumajících prstů, dvoje oči a uši, jeden nos a pusu.
Počítání oddělených objektů nám bývá nejvýš potřebné. Pokud okolí není k počtům nachystané, zavedeme jednotky. Například počet stromů je spočítatelný, kdežto jejich výška vyžaduje stanovit délkovou jednotku. Podobně postupujeme pro teplotu, tlak, čas, inteligenci a další veličiny.
Někteří učenci starověkého světa tušili, že hmota by se mohla skládat z nejmenších jednotek. Pak by byla spočítatelná zcela přesně, podobně jako stromy v lese. Moderní věda přijala tento poznatek jako následek svých pokusů a výpočtů.
Úspěchy fyziky
Nové poznatky 19. století byly snadno k pochopení. Termika: pára táhla vlaky. Elektrotechnika: žárovka ukazovala, co v ní je. A jiskření připomínalo přírodní blesky, včetně zabíjení neopatrných. Záření: rentgenové paprsky prosvěcovaly ruku skrz naskrz. Gravitace: Archimédův zákon dovolil balony, nejpozději i vzducholodě.
Ve 20. století Planck zjistil, že záření je spočítatelné – v zásadě tak, jak stromy v lese. Kousky energie přivedly Einsteina k pozdějšímu zisku Nobelovy ceny. Zato jeho obrovský přínos v prosazení teorie relativity je dodnes v plenkách. Rovnice několika fyzikálních objevitelů fungují, ale co s příčinou? Proč se čas při pohybu zpomaluje?
Když se čas zpomaluje, když se rychlost dvou objektů v pohybu zvláštně sčítá – tak aby rychlost tělesa nepřesáhla rychlost světla, ani jí nedosáhla – co za tím je? Dodnes je to problematika obtížně vnímatelná.
Někdy se lidé domnívají, že když c = konst, pak že se světlo nemůže objektu vzdalovat například rychlostí c/2. Posoudit rychlosti světla mezi více soustavami není snadné. Nabídnu svůj pohled a to příkladem s raketou a paprskem světla.
Od Země letí světelný paprsek do vzdálenosti 300.000 km, kde ho na základně očekává pan Přijímač. Může se tento paprsek vzdalovat, pronásledující raketě, rychlostí c/2?

Obr 1. Paprsek dorazil do Přijímače
Upřesnění ~
Raketa míjí Zemi rychlostí c/2 a přitom vyšle paprsek. Oboje směrem letu k Přijímači. Přijímač pak hodinami změří čas opoždění rakety oproti prve dorazivšímu paprsku (obr. 1, 2).
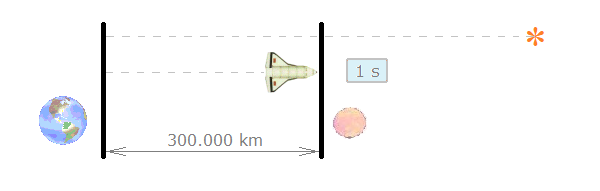
Obr 2. Raketa dorazila do Přijímače
Poznatky ~
(1) Na raketě měří rychlost světa, vždy naměří c.
(2) Pan Přijímač měří rychlost světla, vždy naměří c.
Měření a výpočty ~
(3) Pan Přijímač měří čas t3 od zachycení paprsku do průletu rakety, t3 = 1 s.
Světlo má rychlost c. Známou vzdálenost 300.000 km překonalo za t1 = 1 s. Což sděluje teorie.
Raketa k překonání 300.000 km potřebovala čas t2 = t1 + t3 = 1 + 1 = 2 s.
Rychlost letu rakety v = 300.000 km / 2 s = 150.000 km/s.
Světlo se raketě vzdaluje rychlostí c – v = 300.000 – 150.000 = c/2, což bylo dokázati.
Vysvětlení ~
Raketa ve hmotném světě – dle speciální teorie relativity – je podrobená změnám času a délky, jež souvisí s c = konst.
Raketa ve světové virtuální realitě – dle diskrétní teorie relativity – je podrobená změnám času, jež souvisí s c = konst.
Relativistické skládání rychlostí? ~
Ležák sleduje chodce s jeho rychlostí 4 km/s. Chodec je pomalejší o 6 km/s než cyklista. Tedy cyklista jede rychlostí 10 km/s proti ležákovi. Sčítání 4 + 6 = 10 km/s smíme použít pro malé rychlosti, kdy zanedbáme souvislosti s hraniční rychlostí 300.000 km/s.
Kdežto při rychlostech například: cho = 40.000 km/s, cyk = 60.000 km/s bychom užitím prostého součtu chybovali. Nýbrž by bylo nutné užít relativistického sčítání. Složitější výpočetní vzorec zabrání dosáhnout rychlosti světla (vzorec).
Výše užitý příklad s Přijímačem je odlišný. Sám zná rychlosti obou objektů, takže není potřebné uvažovat relativistické sčítání rychlostí. Tedy případ, kdy první zná rychlost druhého, a druhý zná rychlost třetího. Pak první nepočítá rychlost třetího pouhým jednoduchým součtem.
Závěr
Starověk uvažoval diskrétní (dělenou) stavbu hmoty. A já vyhledávám totéž i samotnému fyzikálnímu prostoru. Rozděluji jej na rozlišená paměťová místa, na síť. Podle vzoru počítače, který údaje uschovává v paměti rovněž bod po bodu.
Kdysi, snad před 15 lety, mi jistý teolog matematik připomínal existenci analogových počítačů. Takové jsem ještě ve škole zažil; před desítkami let byly vhodné pro simulování spojitých procesů. Jenže vždy s méně zaručenou přesností oproti vítězným číslicovým počítačům.
A nyní vzniká otázka, zda snad také celý svět, ve všem všudy, je uspořádaný po jednotlivých bodech. Z takového diskrétního prostoru lze totiž snadným přepočtem přejít přímo do lidského perspektivního vnímání zraku a sluchu. V plné přesnosti, bez nepřesného starověkého Euklidova lineárního prostoru.
Odkazy
[1] Encyklopedie fyziky – Martin Macháček. Vyd. Mladá fronta, Praha 1995, s.215
[2] www.tichanek.cz – Geometrické modely časoprostoru
Bohumír Tichánek
Poslední články autora:


