1. Úvod
Velmi dlouho vystihujeme podobu světa lineárním Euklidovým prostorem.
Objevy teorie relativity ukázaly nečekané souvislosti. Proměny času jsou snadněji uvěřitelné než délkové změny hmoty a prostoru. Jsou prokázané i technicky. Přitom výpočty bývají docela jednoznačné. Žijeme tedy v gumovém Vesmíru? Proměnné délky nám snad mají prokazovat virtuální realitu našeho světa?
„Einstein ukázal, že předměty pohybující se rychlostí blízkou rychlosti světla se stojícímu pozorovateli jeví jako rozplácnuté ve směru svého pohybu. Jde o čistě relativistický efekt: těleso se ve skutečnosti nijak nezmenšuje, pouze se tak jeví pozorovateli.“ [1]
„Tvar kvádru se změní tak, že hrana rovnoběžná se směrem pohybu se zkracuje, zatímco délky ostatních hran zůstanou nezměněny. — Opět připomínáme, že tyto výsledky jsou důsledky Lorentzovy transformace a nevypovídají nic o tom, jaký tvar bychom skutečně pozorovali.“ [2]
Zde vstoupím do problematiky jinými dveřmi. Vše přitom zůstane výpočetně podložené. Zlepší se snad pochopitelnost axiomů?
2. Jinak
Zkouším alternativně posuzovat svět geometrií perspektivního zrakového vnímání. Vjemy podkládám diskrétním prostorem (nespojitými body „šachovnice“), tedy v absolutní přesnosti [3]. Bezrozpornost spojitého Euklidova prostoru je menší, protože tamní výpočty bývají často bezvýsledné. Přesto tradičně souhlasíme s pouhým zaokrouhlením výpočtů iracionalit, jež mají vysvětlovat náš svět.
Zmíněný diskrétní prostor ať tvoří 3D prostorovou síť. Její sousední uzly v ní vytvářejí vzdálenost asi
10-34 metru, dle Planckovy délky.
3. Příklad pohybu podsvětelnou rychlostí
Vesmírem kdesi letí kamínek, meteorit. Má rychlost 0,9c. Vedle něho, rovnoběžně, proletí stejným směrem i paprsek světla. My na Zemi víme, že rozdíl rychlostí mezi nimi je:
c – 0,9c = 0,1c
Pokud má kamínek informace ze Země, pak rozumuje – jak se mu paprsek může vzdalovat rychlostí „c“, dle určení speciální teorie relativity (STR)? Toto upřesním dvěma modely.
4. Zdroj pulsů
Zavádím mimovesmírný Zdroj pulsů. Tato časová základna ať podkládá náš svět opakovanými pulsy (PE); trvání každého posuzujeme přibližně 10-43 s. Podkládají pohyb (PL), anebo nevyužité k pohybu (PT) naopak čas.
Důsledky hypotetického Zdroje pulsů jsou v souladu s: „Kterýkoli fysikální jev může být užit jako hodiny, za předpokladu, že se může opakovat přesně a libovolně často.“ [4]
Posoudím neproměnnost rychlosti „c“, ovšem neodvodím ji zde z Michelsonova měření, nýbrž z bodového modelu.
5. Provedení grafu
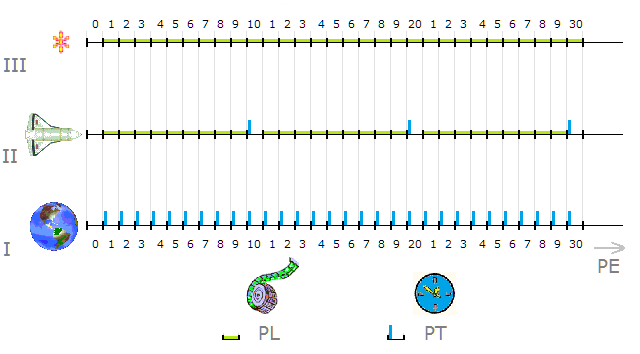
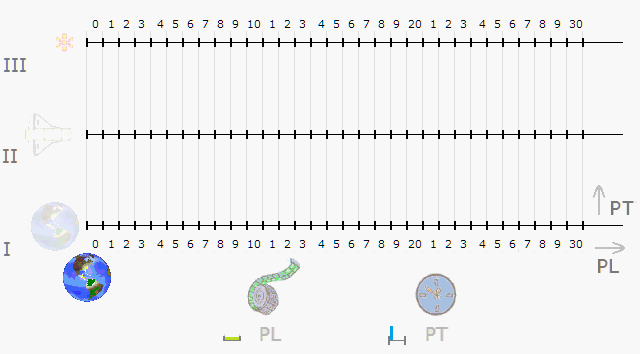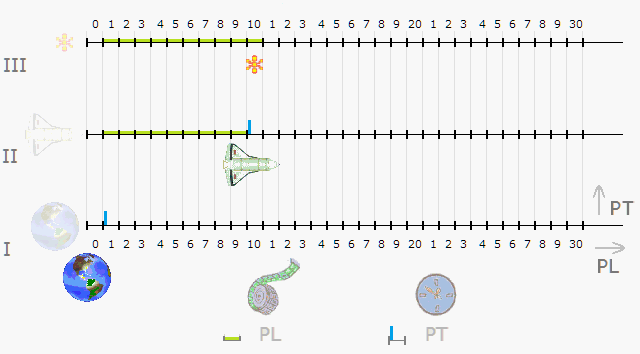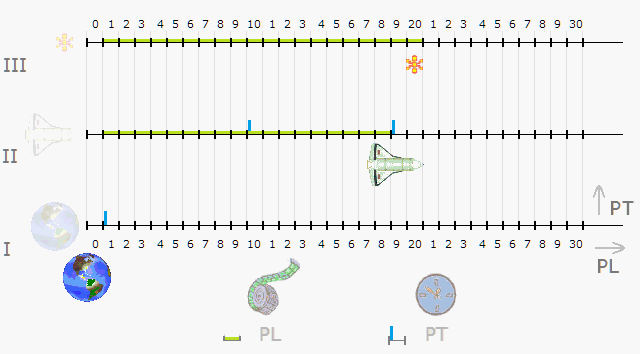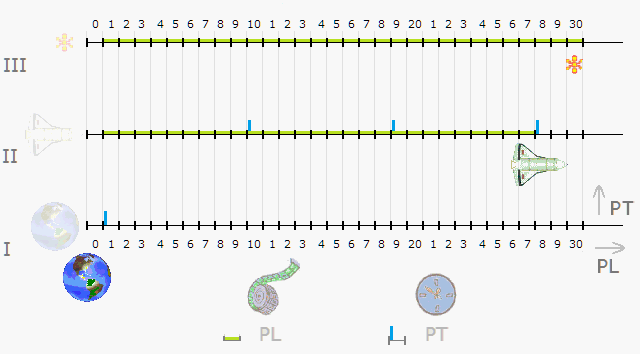
Obr. 1. Třicet Zdrojových pulsů (PE) pro foton, koráb a Zem. Využity na pulsy délky (PL) nebo času (PT)
Pulsy vznikají jeden po druhém, stále znovu. V grafu (obr. 1):
- vodorovně se nanášejí pulsy PL (zeleně), určené k posunování bodů hmoty v posicích
- svisle jsou kreslené pulsy časové (PT) – nevyužité.
Tento graf sleduje využití pulsů, kdežto pohyb bodů 1D prostorem je umístěný níž (obr. 2).
6. Hodnocení rychlostí pohybu
Rychlost světla: c = 1 PL/1 PT {1}
→ II … Země hodnotí rychlost korábuKorábu (II), v jeho translaci, se stále opakuje využití bloku 10 pulsů.
Zeměkoule (I) se nepohybuje. Všechny zdrojové pulsy PE využije jako časové PT. Během 10 pozemských PT (1. až 10. v lince I) koráb devětkrát přeskočí délku PL (1. až 9. puls v lince II). Z toho vychází rychlost korábu vůči Zemi, dráha lomeno čas:
vI-II = 9 PL/10 PT = 0,9c {2}
→ II → III … Země hodnotí vzdalování fotonu od korábuVýsledek {2} odečtu od {1}. Tedy od rychlosti fotonu odečtu rychlost korábu, obojí hodnoceno ze Země. Foton uniká korábu rychlostí:
vI-II-III = c – 0,9c = 0,1c {3}
Pozemšťané hodnotí menší rychlosti korábu, oproti světlu, o 0,1c. To je snad v rozporu se STR? Zatímco na korábu jim zaostávání určuje rychlost c, dle axiomu STR?
→ III … Země hodnotí rychlost fotonuZeměkoule hodnotí rychlost světla. V kterémkoliv z 30 PE; na každý PL fotonu připadá 1 PT Zeměkoule. Například ve 21. PE, ve shodě s {1}:
1 PL/1 PT = c {4}
→ III … Koráb posuzuje rychlost fotonuV délkových pulsech PL uvnitř korábu žádný pohyb není; ustane i rozumová činnost tvorů. Probíhá translace celého korábu. Pracovat a přemýšlet tam mohou jen v časových pulsech PT; využitím je mění v PL. Na korábu v časových pulsech 10., 20. a 30. změří rychlost světla a potřikrát zjistí fotonu přeskoky PL (obr. 1). Tedy 3 PL/3 PT = c.
Toto popisované informatické řešení souhlasí s pohybem světla konstantní rychlostí „c“, určenou STR. Avšak zde diskrétní model nabízí vzdalování jen v časových úsecích PT, takže skutečný růst vzdálenosti je pomalejší, menší než odpovídá „c“. V souladu s pozemským hodnocením {3}. Prostě v délkových pulsech PL foton korábu neuniká.
Nabízí se krátce:
Světlo letí prázdným prostorem vždy rychlostí „c“. {Definice 1}
Navržený diskrétní přístup je jednoduchý – nepotřebuje změny délek okolní hmoty, závislé na rychlosti, dle spojité STR. Uznává pouze změny vnímání, viz jiné autorovy soubory [5].
7. Model srovnává rychlosti
Předchozí model ukazoval využití zdrojových pulsů, kdežto rychlost byla počítaná. Další model, fázovaný, nabídne smyslový názor na rychlost. Vodorovné osy I, II, III nyní vyjadřují délku PL v bodovém prostoru pro tři objekty.
Koráb (II) s fotonem (III) a Zeměkoulí (I) se v grafu uplatňují každý jen bodem – zařazením do jediné posice. V časovém pulsu (modrém) se bod neposune, neobsadí následující posici. Tu může obsadit některým z pozdějších Zdrojových pulsů PE.
Obr. 2. Pohyb diskrétním prostorem
Účinek diskrétních bodů na vnímání tvora vyžaduje převod do perspektivního zrakového prostoru [3]. Výpočty vycházejí v plné přesnosti, ve srovnání s nepřesnými iracionalitami Euklidova prostoru.
8. Shrnutí
Seřadím odhadované výhody předloženého diskrétního posuzování Vesmíru.
- Konstantní rychlost světla ve vakuu je zdůvodněna činností Zdroje. Netřeba jen usuzovat, jako je tomu u Michelsonova zjištění stavu proužků světla.
- Axiom relativistického času, se kterým technika 20. století pracuje, je zde zdůvodněn bez nutnosti změn geometrických délek vesmírného prostoru a hmoty ve spojité STR.
- Veličina čas, dlouhodobě neuchopitelná, se přibližuje fyzikálnímu vysvětlení v bodovém vyjádření. Ovšem námi vnímaný čas (sekundy) vyžaduje převod časových pulsů (PT) do perspektivního vyjádření [6].
- Perspektivní vyjádření času zdůvodňuje zvýrazněnou, lidem známou, přesvědčivou časovou přítomnost. Rozdílnou od minulosti a budoucnosti.
- Rychlost světla je konstantní jen vůči prostorové síti, a nikoliv vůči pozorovateli – nabízejí modely tohoto článku. Je to opakem oproti dávno zvažované a odmítnuté balistické hypotéze.
- Použitý diskrétní přístup zdůvodňuje a obhajuje zásadní rozdíl změřené světelné rychlosti vždy „c“ (soustava KAMINEK) a naproti tomu posuzování rychlosti světla z odlišné inerciální soustavy – jinak než „c“ (soustava ZEMĚ).
9. Závěr
Lze zvažovat, zda popsané informatické postupy pro STR se přibližují kvantové mechanice.
„V Einsteinově vědecké činnosti ještě pár let po „zázračném roce“ 1905 nic nenasvědčovalo tomu, že se ústředním tématem jeho života má stát gravitace. Naopak by se dalo očekávat, že bude stržen spojováním speciální teorie relativity s kvantovými idejemi, které byly v popředí zájmu jeho kolegů a těsně souvisí s pokrokem experimentální fyziky.“ [7]
Literatura, odkazy
[1] Šíp času – Peter Coveney, Roger Highfield. Nakl. Oldag, Ostrava 1995, s. 88
[2] Základy teorie relativity – Novotný, Jan – Jurmanová, Jana – Geršl, Jan – Svobodová, Marta. Masarykova univerzita, Brno, s. 51
[3] Interakce prostorů – IIIv – B. Tichánek. Převod bodů z diskrétního do spojitého perspektivního prostoru
[4] Fysika jako dobrodružství poznání – Einstein, A., Infeld, L. Vydavatelstvo Družstevní práce, Praha 1945 (něm. 1938), s. 174
[5] 6. Délky, hmotnost, kruhový pohyb – B. Tichánek. Ve vysoké rychlosti hmota nedilatuje, leč změní se vjemy pozorovatele
(Lorentzovo zkráceni.gif – graf. V diskrétním prostoru lze vnímat jen v časových okamžicích)
[6] Zdůvodnění speciální teorie relativity hypotetickým pulsním zdrojem – B. Tichánek. Obsahuje 4 grafy
Spojité perspektivní vnímání s vyznačením rastru.gif – graf. Časová perspektiva ozřejmí zbytnělý lidský pocit časové přítomnosti
[7] 100 let obecné teorie relativity – Jan Novotný, Brno. Pokroky matematiky, fyziky a astronomie, ročník 60 (2015), č. 3, s. 178
Bohumír Tichánek
Poslední články autora:


